calculus-sc1801

这篇文章已经 1099 天没有更新了，内容可能已经过期了

课程大纲

介绍

课程概览

课程包括的话题：

• Concepts of Function, Limits and Continuity 函数，极限，连续性的概念
• Differentiation Rules, Application to Graphing, Rates, Approximations, and Extremum Problems 微分规则，图形应用，比率，近似和极值问题
• Definite and Indefinite Integration 定积分和不定积分
• The Fundamental Theorem of Calculus 微积分基本定理
• Applications to Geometry: Area, Volume, and Arc Length 几何应用：面积，体积和弧长
• Applications to Science: Average Values, Work, and Probability 科学应用：平均值，功和概率
• Techniques of Integration 积分的技巧
• Approximation of Definite Integrals, Improper Integrals, and L’Hôspital’s Rule 定积分的近似值，瑕积分，洛必达法则

课程目标

完成此门课程后，应该对单变量微积分的基本概念和一系列技能有清晰的理解，能够有效地使用这些概念。

基础的概念如下：

1. 导数(Derivative)（变化率），计算为比率的极限；
2. 积分( Integral)（和），计算为黎曼和(Riemann sum)的极限。

需要拥有的能力：

• Use both the limit definition and rules of differentiation to differentiate functions.
• 使用极限定义和微分规则来区分函数。
• Sketch the graph of a function using asymptotes, critical points, the derivative test for increasing/decreasing functions, and concavity.
• 使用渐近线，临界点，增、减函数的导数测试和凹度绘制函数图形。
• Apply differentiation to solve applied max/min problems.
• 应用微分解决给定的最大、最小值问题。
• Apply differentiation to solve related rates problems.
• 应用微分解决相应的变化率问题。
• Evaluate integrals both by using Riemann sums and by using the Fundamental Theorem of Calculus.
• 通过使用黎曼和和微积分的基本定理来计算定积分的值。
• Apply integration to compute arc lengths, volumes of revolution and surface areas of revolution.
• 应用积分来计算弧长，旋转体积和旋转表面积。
• Evaluate integrals using advanced techniques of integration, such as inverse substitution, partial fractions and integration by parts.
• 使用高级定积分技巧来计算定积分，比如逆代换，部分分式积分，部分积分。
• Use L’Hospital’s rule to evaluate certain indefinite forms.
• 利用洛必达法则来计算某些不定型。
• Determine convergence/divergence of improper integrals and evaluate convergent improper integrals.
• 确定瑕积分的收敛或发散，然后计算收敛的瑕积分。
• Determine the convergence/divergence of an infinite series and find the Taylor series expansion of a function near a point.
• 确定无穷级数的收敛或发散，并找到一个点附近函数的泰勒级数展开。

1. 微分（DIFFERENTIATION）

Part A ：定义和基础规则

Session 1：导数（Derivative）介绍

Clip 1

什么是导数？从几何解释（ geometric interpretation）和物理解释（physical interpretation）分别展开来讲。

---

Clip 2 微分的几何解释

从几何上来看：

$$f\mathrm{在}{x}_0\mathrm{处}\mathrm{的}\mathrm{导}\mathrm{数}{f}^{{}^{\prime }}(x_0)，\mathrm{就}\mathrm{是}\mathrm{函}\mathrm{数}y=f(x)\mathrm{在}\mathrm{点}P=(x_0,f(x_0))\mathrm{处}\mathrm{的}\mathrm{切}\mathrm{线}\mathrm{的}\mathrm{斜}\mathrm{率}。$$

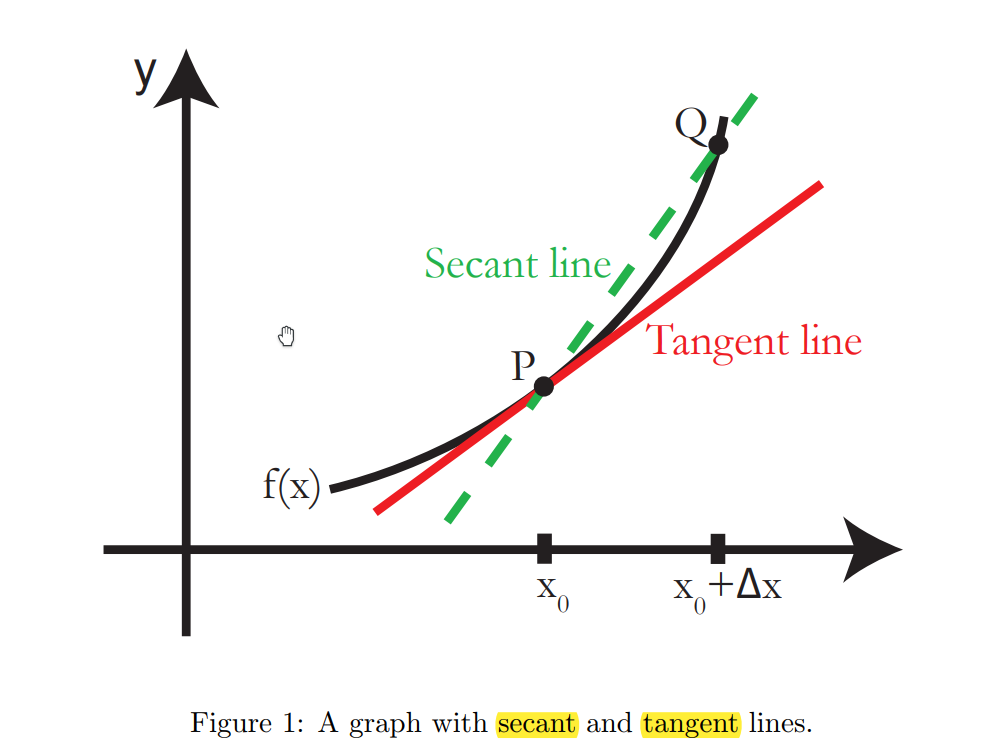
什么是切线（tangent line）？

• 不仅仅是与函数图像只有一个交点的直线；
• 也是函数$f(x)$的图像经过$P=(x_0,f(x_0)),Q$的割线（SECANT），当Q接近于P的极限。

同时，我们知道函数的公式时，可以通过点斜式和上述定义求出函数位于$P=(x_0,f(x_0))$处的切线公式：
$y-y_0=m(x-x_0)$，其中，$m=f^{‘}(x_0)$。

定义：$f\mathrm{在}{x}_0\mathrm{处}\mathrm{的}\mathrm{导}\mathrm{数}{f}^{{}^{\prime }}(x_0)，\mathrm{就}\mathrm{是}\mathrm{函}\mathrm{数}y=f(x)\mathrm{在}\mathrm{点}P=(x_0,f(x_0))\mathrm{处}\mathrm{的}\mathrm{切}\mathrm{线}\mathrm{的}\mathrm{斜}\mathrm{率}。$

---

Clip 3 割线的极限

割线是指与曲线图像有两个交点的直线。如果两个交点相距的非常近，那么，割线的斜率就与曲线的斜率近似相等。我们想要找到切线的斜率m—与曲线的斜率相等—那么可以利用割线的斜率来求出。

假设直线PQ是函数$f(x)$图像上的一条割线，函数图像在P点处的斜率，可以通过Q不断靠近P点的方式，由直线PQ的斜率求得。

（函数图像在P点处的）切线就等于当Q$\to$P时的割线PQ。

---

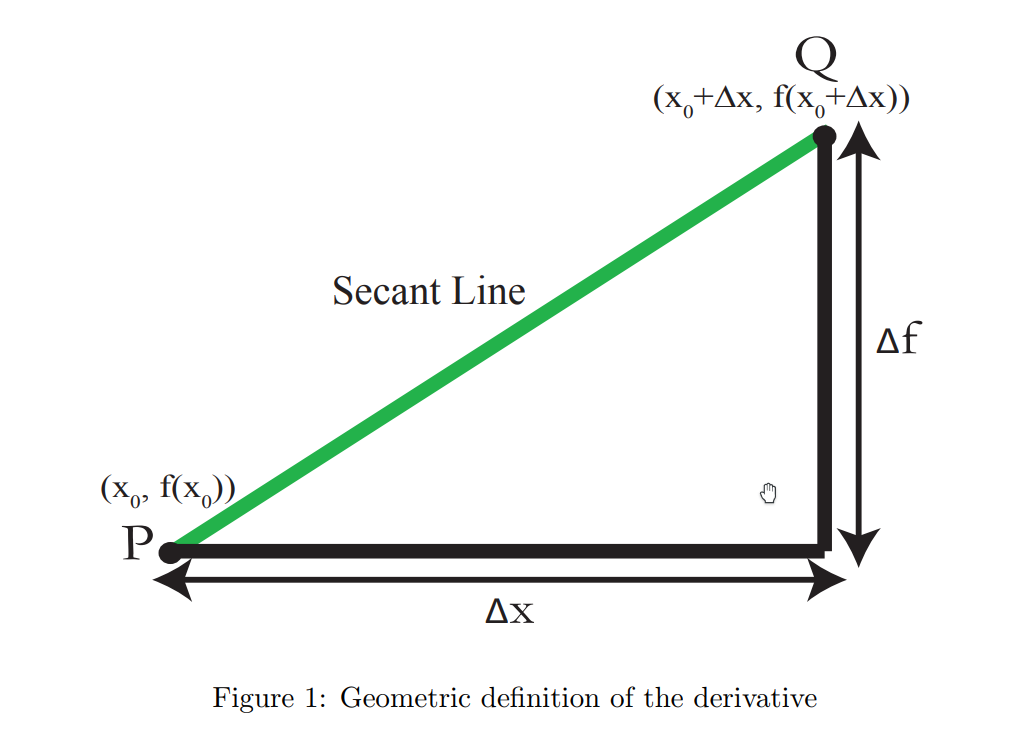
Clip 4 以比率作为斜率

从函数$f(x)$的图像上一点$P(x_0,f(x_0)$，开始，水平移动一个很小的距离$\mathrm{\Delta }x$,找到图像上另一点$Q(x_0+\mathrm{\Delta }x,f(x_0+\mathrm{\Delta }x))$,PQ即为函数图像的一条割线。P、Q两点的垂直距离$\mathrm{\Delta }f=f(x_0+\mathrm{\Delta }x)-f(x_0)$。

由前述可知，切线是割线的极限，所以可知切线的斜率也是割线的斜率的极限。

割线的斜率，可由$\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}$。

所以，切线的斜率：

​ $m=\underset{Q\to P}{lim}\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}$

---

Clip 5 主要公式

由图中，可知$Q=(x_0+\mathrm{\Delta }x,f(x_0+\mathrm{\Delta }x))$,所以

$$m=\underset{\mathrm{函}\mathrm{数}f\mathrm{在}{x}_0\mathrm{处}\mathrm{的}\mathrm{导}\mathrm{数}}{\underbrace{f^{{}^{\prime }}(x_0)}}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}=\underset{\mathrm{差}\mathrm{商}（differencequotient）}{\underbrace{\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x_0+\mathrm{\Delta }x)-f(x_0)}{\mathrm{\Delta }x}}}$$

---

切线和割线习题

Secant Approximation mathlet

1. (a)

   | $\mathrm{\Delta }x$ | -0.5 | -0.25 | 0.25 | 0.5 |
   | :—————————————-: | :—-: | :—-: | :—-: | :—-: |
   | $\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}$ | -0.53 | 0.16 | -0.41 | -0.59 |

   (b) $\frac{dy}{dx}=-0.16$

   (c) $[-0.1,0.18]$

2. (a)
   | $\mathrm{\Delta }x$ | -0.5 | -0.25 | 0.25 | 0.5 |
   | :—————————————-: | :—-: | :—-: | :—-: | :—-: |
   | $\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}$ | -0.88 | -0.97 | -0.97 | -0.88 |

   (b) $\frac{dy}{dx}=-1.0$

   (c) $[-0.46,0.46]$

3. (a)
   | $\mathrm{\Delta }x$ | -0.5 | -0.25 | 0.25 | 0.5 |
   | :—————————————-: | :—-: | :—-: | :—: | :—: |
   | $\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}$ | -0.59 | -0.41 | 0.16 | 0.53 |

   (b) $\frac{dy}{dx}=-0.16$

   (c) $[-0.1,0.18]$

4. (a) 不一样；

---

额外的习题视频

$f(x)=\frac{1}{1+x^2}$，画出$f(x)$的图像，并求出$f^{‘}(x)$。

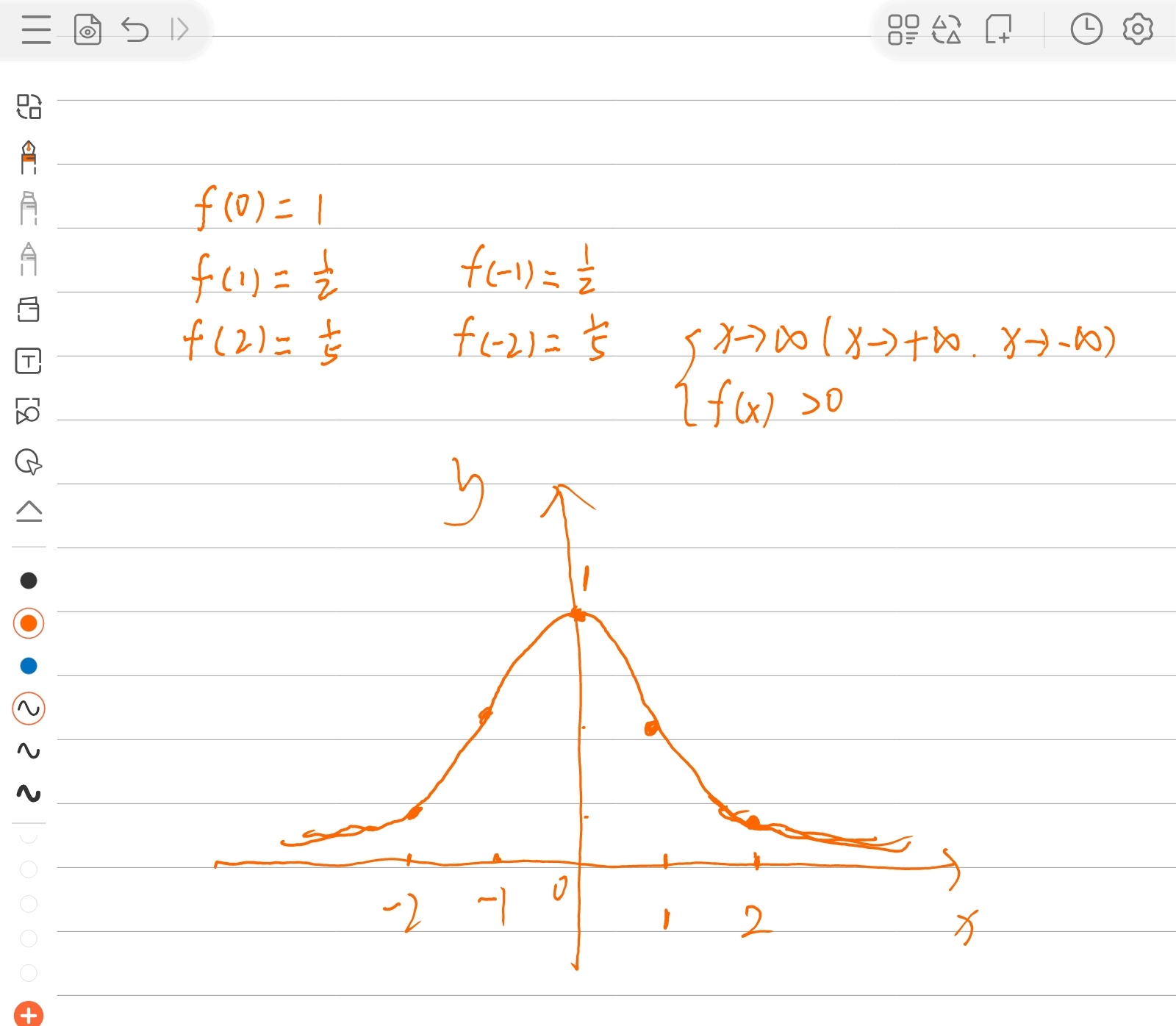
可以看出$f(x)$是一个偶函数，代入如下几个点，大致描绘出函数图像

x	f(x)
-2	1/5
-1	1/2
0	1
1	1/2
2	1/5

注意$x\to \text{infin}(x\to +\text{infin}\mathrm{或}\mathrm{者}x\to -\text{infin})$时，f(x)恒大于0.

---

导函数的图像

1. 找出导数为0的点-原函数的顶点；
2. 函数增区间，表示导数大于0；函数减区间，表示导数小于0；
3. 距离导数为0的点最远的值也是图像最陡的地方，为导函数的顶点。

---

Session 2：导数举例

这一目将会运用主要公式来求函数$\frac{1}{x}\mathrm{和}{x}^n$的导数。并且学习导数的另一种书写方式。

Clip 1 例子1 y=1/x

---

Clip 2 难题：位于y=1/x的图像下的三角形

---

Clip 3 导数表示方法

---

Clip 4 y=x^n

二项式定理：

$$\begin{array}{rl}& (a+b{)}^n={\displaystyle \sum _{r=1}^n{C}_n^r{a}^{n-r}{b}^r}\\ & \mathrm{其}\mathrm{中}{C}_n^r=\frac{n!}{r!(n-r)!},\mathrm{又}\mathrm{有}(\genfrac{}{}{0ex}{}{n}{r})\mathrm{的}\mathrm{记}\mathrm{法}，\mathrm{叫}\mathrm{作}\mathrm{二}\mathrm{项}\mathrm{式}\mathrm{系}\mathrm{数}。\end{array}$$